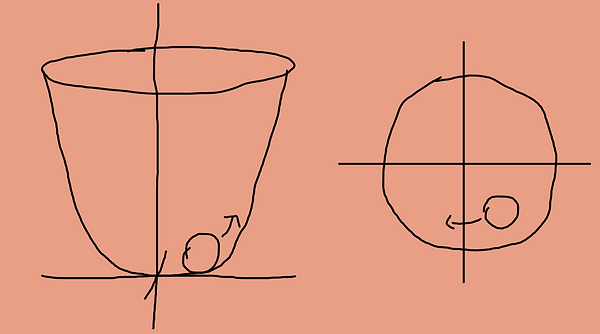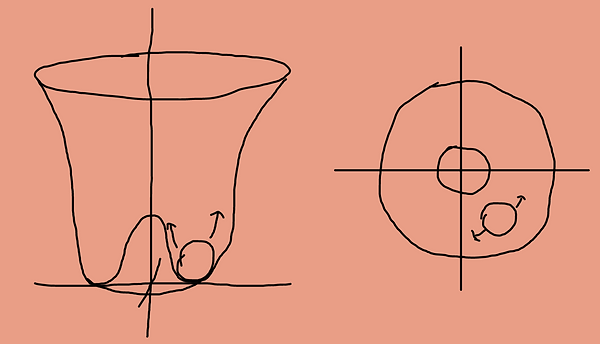The Higgs Fields

You may have noticed that there is one particle in the standard model that we have not yet talked about. The final particle that we will look at is the Higgs Boson, which comes from the Higgs Field.

The higgs boson is not a gauge boson, but rather a scalar boson having a spin of 0. The higgs boson is also the reason to why the W and Z bosons are so abnormally massive. In fact, gauge bosons shouldn't have mass at all. This is because the higgs field has a vital role in giving the other particles their mass.

From now on, things will be a bit more abstract, so do your best to follow along. Let's first go over spontaneuos symmetry breaking again, but with more detail.

In the case of a ball in a valley, its motions are symmetrical from left to right.

However, in the case of a valley with a hill in the middle, the ball drop into one of the smaller valleys, causing a state of broken symmetry.

In a similar way, the universe's symmetry broke and a grand unified force broke symmetry into different forces.

For now, let's put the hill with a valley on an x-y coordinate system. Note that the ball is constantly below zero.

What if we make the original valley 3d, so it is now a bowl? The bowl has a new continuous symmetry so that if you rotate it, it stays the same. We can say that this is global U(1) symmetry. If you recall, this is the same symmetry group that electromagnetism is under. If we want to have the same conditions as the one for electromagnetism, we need local U(1) invariance. That is to say, the system does not change under U(1) local symmetry. Mathematically, we would add a gauge field (electromagnetism) that allows for this new rotational degree of freedom, and in this situation, the new degree of freedom requires no energy and therefore the corresponding gauge boson (the photon) is massless.

Now let's do the same for the valley with a hill. This new graph is called "Mexican Hat Potential". Like before, if the ball rolled into on of the valleys, it would cause a state of broken symmetry. Each point on the valley the ball is in is a different physical state. While it is in broken symmetry, it still keeps the shape of the U(1) symmetry.

In this senario, the ball can oscilate not only up and down, but rotationally. This produces bosons called Goldston bosons. These Goldston Bosons are massless.

Also, now that the ball is below zero, it causes a non-zero vacuum expectation value. The ball has freedom in oscilating up and down along the smaller valley, causing the Higgs boson. Because of the non-zero vacuum expectation value, there is a little bit of "higginess" everywhere.

When we try to map the mexican hat potential in the same way as before, there is a more complex situation. The goldstone bosons sort of get abosrbes by the gauge bosons, giving them mass.

When we do this for the electroweak field under U(1)xSU(2) invarience, we get three Goldstone Bosons that are abosrbed by the W and Z bosons, giving them their abnormal mass. The photon is massless.

The takeaways (TLDR):

The higgs field gives particles their mass.

It causes the W and Z bosons to have mass along with spontaneuous symmetry breaking.