The Nature of Particles

Particle Physics -- and Quantum Physics - are weird. As a result, an open mind helps significantly in understanding these topics.

​

Here are some topics you need to know:

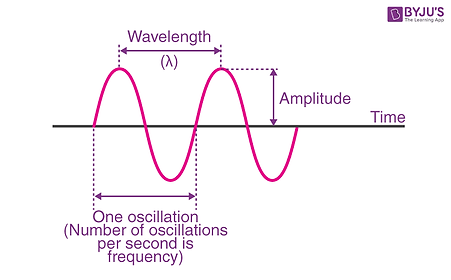
Electromagnetic radiation is light. For now, think of light as a wave. 

​

​

​

​

​

​

​

​

​

​

​

​

Image from: https://byjus.com/jee/properties-of-waves/

​

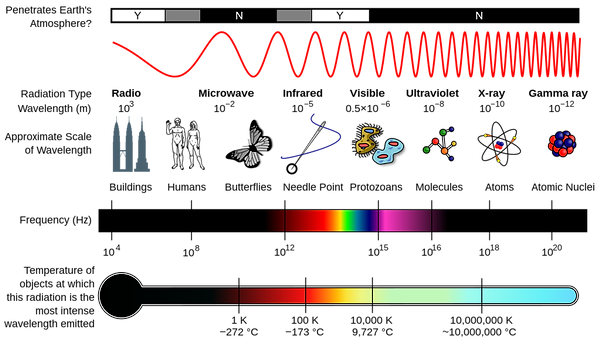
The frequency is how bright the light is (speed of the wave), and the wavelength decides the "color" of the light. Here is the electromagnetic spectrum, or all the "colors" light can have based on their frequency.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

Image from: https://en.wikipedia.org/wiki/Electromagnetic_spectrum​

​

Okay. Now that we've gotten some background out of the way, let's begin with Black--body Radiation, a topic that will bring us from Classical Physics, the physics that we know, to Quantum Physics, the physics that deals with the quantum world.

​

All objects in the universe emit energy as light. The amount of energy depends on factors such as color or temperature. The more temperature, the more energy, and the more the average frequency of electromagnetic radiation (light) emitted.

​

So what is a black body? A black body is a theoretical object that absorbs all electromagnetic radiation and stays in thermal equilibrium with its surroundings. As a result, the light emitted is determined by only the temperature of the body. However, this quickly led to problems. According to Classical Physics, the black body would emit the same amount of light for each frequency, leading to an infinite amount of energy being emitted. This failure of classical mechanics was called the ultraviolet catastrophe.

​

This problem was solved by Max Planck, who came up with the idea that objects emit electromagnetic radiation in small packets called quanta rather than continuously. The size of the quanta is given by:

​

E = h * f

​

E is energy, the size of the quanta, f is the frequency, and h is the Planck Constant 6.626 * 10^-34. It is increasingly more difficult to emit higher frequencies, and the energy is limited to low levels of light. This quantization of energy is an important feature of quantum physics.

​

 

Now let's get into something a bit more interesting. The Double Slilt Experiment was an experiment conducted by Thomas Young in order to show the wave/particle nature of light. However, it also led to key understandings of the quantum world. It used a behavior of waves called diffraction in order to do this.

​

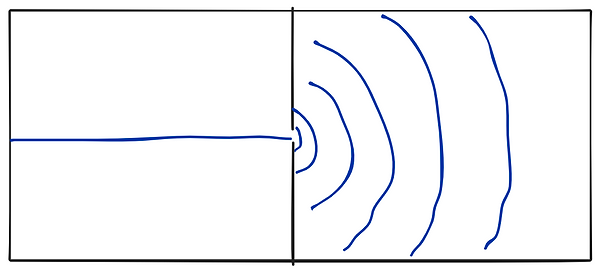
Imagine a pool of water, and a wall dividing it in 2. The wall has a slit in the middle separating it into two parts. As a wave travels through that slit, it experiences a sort of rippling effect, as shown below.

​

​

​

​

​

​

​

​

​

​

​

​

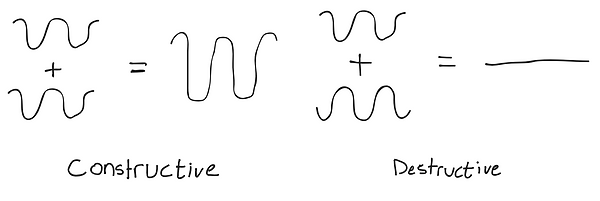
There is also another behavior of waves that you need to know, Interference. Interference is when two waves interact and add their displacement at every point. Constructive Interference is when the resulting wave grows larger, and Destructive Interference is when those two waves cancel out.

​

​

​

​

​

​

​

​

​

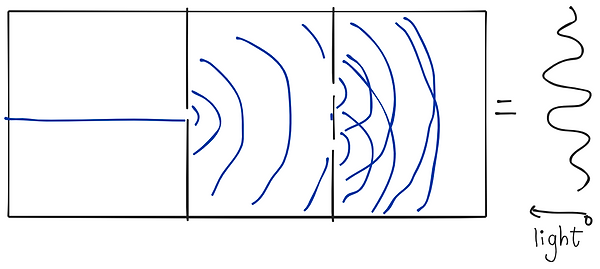
Here is the Setup of the Double Slit Experiment. the wave passes through one wall with a singular slit and diffracts into another wall with two slits. The wave diffracts twice more, and the now two waves interfere constructively and destructively. The result is an interference pattern in the wave once it gets to the wall.

​

​

​

​

​

​

​

​

​

​

​

Now, imagine instead of water, we use light. We fire a stream of photons instead of the wave, and the interference pattern still forms, showing the wave-like behavior of photons.

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

​

Here's where things get weird. What if we fire photons (particles of electromagnetic radiation/light) one at a time? Your intuition says that the interference pattern would no longer form as the photons have nothing to interfere with. Furthermore, photons are elementary particles, meaning that they cannot split into two, go into both slits in the second wall, and interfere. However, the interference pattern still forms. One at a time, particles seem to avoid areas that aren't lit up and hit areas that are lit up.

​

Why does this happen? The answer lies in something called the wave function (represented by ψ). The wave function can be described as a wave of probability, or a wave of possibility. One way you can imagine it is the sum of all the possible paths of a particle (taking into account its position and momentum), except that these different paths can interact with each other. The result is a wave of the probability of the paths the particle can take. When we say paths, that include the particle's change in state -- its change in properties such as position, energy, and momentum.  It is also important to know that the wave function does not just apply to light, but to all particles.

​

When a particle is observed, the wave function collapses as settles on a singular state. In the Double Slit Experiment, the wave function collapses when we fire the particle and when the particle hits the wall. This collapse also occurs when we try to measure a particle's properties.

​

Classical physics is known to be deterministic, meaning that with enough information, you can predict the future. However, Quantum physics is indeterministic, meaning that it cannot be predicted. This arises from the question: in the Double Slit Experiment, how does a particle decide which slit to go through? The answer is that there is no mechanism that causes this. The universe decides a path based on probability. This caused much discussion in the physics community. Albert Einstein even said, "God does not play dice with the universe".

​

The Schrödinger equation describes how the wavefunction of a particle changes over time. I'm not going to show you the math because it's a bit hairy, but feel free to search it up yourself.

​

Another important quantum mechanics phenomenon is quantum superposition. quantum superposition says that an object not being observed is in all possible states at once, meaning that it can have different properties at the same time. its superposition is a combination of every state it can be in. It is easier to visualize this when we take into consideration the wave function. when the particle is not observed -- when its wave function hasn't collapsed -- it exists at all possible states.

​

Ultimately, it's more useful to determine the probability of a particle being in a certain place than its actual location.
 

Another important concept to know is the Heisenberg Uncertainty Principle. It basically says that the more we know about a particle's position, the less we can know about its momentum. This is the same for energy and time. It is impossible to know both position and momentum at same time, and energy and time at the same time. In the equation, Δx is the error in position, Δp is the error in momentum, ΔE is the error in energy, Δt is the error in time, and ħ is the reduced Planck constant, 6.582119569 * 10−16 eV⋅s.

​

​